1. зміст
2. Історія виникнення теорії графів
3. Термінологія теорії графів
4. Зображення графів на площині
5. Деякі задачі теорії графів
6. література
7. задачники
8. Примітки
9. Див. також

https://ru.wikipedia.org/wiki/Теория_графов

Теорія графів - розділ дискретної математики , Що вивчає властивості графів . У загальному сенсі граф представляється як безліч вершин (вузлів), з'єднаних ребрами. У строгому визначенні графом називається така пара множин. 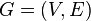, де 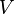є підмножина будь-якого рахункового безлічі, а 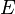- підмножина .

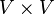Теорія графів знаходить застосування, наприклад, в геоінформаційних системах (ГІС). Існуючі або знову проектовані будинки, споруди, квартали і т. П. Розглядаються як вершини, а що з'єднують їх дороги, інженерні мережі, лінії електропередач і т. п. - як ребра. Застосування різних обчислень, вироблених на такому графі, дозволяє, наприклад, знайти найкоротший об'їзний шлях або найближчий продуктовий магазин, спланувати оптимальний маршрут.

Теорія графів містить велику кількість невирішених проблем і поки не доведених гіпотез.

зміст

Історія виникнення теорії графів

Родоначальником теорії графів вважається Леонард Ейлер . У 1736 році в одному зі своїх листів він формулює і пропонує рішення завдання про семи Кенігсбергськая мостах , Що стала згодом однією з класичних задач теорії графів.

Термінологія теорії графів

Термінологія теорії графів понині не визначена строго. Зокрема, в монографії Гудман, Хідетніемі, 1981 сказано: «В програмістські світі немає єдиної думки про те, який із двох термінів" граф "Або" мережа ". Ми вибрали термін "мережа", так як він, мабуть, частіше зустрічається в прикладних областях ». Аналогічна ситуація з термінами « вершина / точка ».

Зображення графів на площині

При зображенні графів на малюнках найчастіше використовується наступна система позначень: вершини графа зображуються точками або, при конкретизації сенсу вершини, прямокутниками, овалами і ін., Де всередині фігури розкривається зміст вершини (графи блок-схем алгоритмів ). Якщо між вершинами існує ребро, то відповідні точки (фігури) з'єднуються лінією або дугою. У разі орієнтованого графа дуги замінюють стрілками, або явно вказують спрямованість ребра. Іноді поруч з ребром розміщують пояснювальні написи, що розкривають сенс ребра, наприклад, в графах переходів кінцевих автоматів . Розрізняють планарниє і непланарние графи. планарний граф - це граф, який можна зобразити на малюнку (площині) без перетинання ребер (найпростіші - трикутник або пара пов'язаних вершин), інакше граф непланарний. У тому випадку, якщо граф не містить циклів (що містять, принаймні, один шлях одноразового обходу ребер і вершин з поверненням в початкову вершину), його прийнято називати «Деревом» . Важливі види дерев в теорії графів - бінарні дерева, де кожна вершина має одне вхідне ребро і рівно два виходять, або є кінцевою - не має виходять ребер і містить одну кореневу вершину, в яку немає вхідного ребра.

Не слід плутати зображення графа з власне графом (Абстрактної структурою), оскільки одному графу можна зіставити не одне графічне представлення. Зображення покликане лише показати, які пари вершин з'єднані ребрами, а які - ні. Часто на практиці буває важко відповісти на питання, чи є два зображення моделями одного і того ж графа чи ні (іншими словами, ізоморфні Чи відповідні зображенням графи). Залежно від завдання, одні зображення можуть давати більш наочну картину, ніж інші.

Деякі задачі теорії графів

До теорії графів також відноситься цілий ряд математичних проблем, не вирішених на сьогоднішній день .

література

• Дістель Р. Теорія графів Пер. з англ. - Новосибірськ: Видавництво інституту математики, 2002. - 336 с. ISBN 5-86134-101-X .
• Diestel R. Graph Theory, Electronic Edition . - NY: Springer-Verlag, 2005. - С. 422.
• Басакер Р., Саати Т. Кінцеві графи і мережі. М .: Наука, 1974. 368c.
• Бєлов В. В., Воробйов Є. М., Шаталов В. Є. Теорія графів. - М.: Вища. школа, 1976. - С. 392.
• Берж К. Теорія графів та її застосування. М .: ІЛ, 1962. 320c.
• Емелічев В. А., Мельников О. І., Сарванов В. І., Тишкевич Р. І. Лекції з теорії графів. М .: Наука, 1990. 384с. (Изд.2, испр. М .: УРСС, 2009. 392 с.)
• Зиков А. А. Основи теорії графів . - М.: «Вузівська книга» , 2004. - С. 664. - ISBN 5-9502-0057-8 . (М .: Наука, 1987. 383c.)

• Хімічні додатки топології і теорії графів. Під ред. Р. Кінга. Пер. з англ. М .: Мир, 1987.

• Кірсанов М. Н. Графи в Maple. М .: Физматлит, 2007. 168 c. /upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini-file_acrobat.gif "target =" _blank "> https://upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini -file_acrobat.gif)! important; background-attachment: initial! important; background-color: initial! important; background-size: initial! important; background-origin: initial! important; background-clip: initial! important; background- position: 100% 50%; background-repeat: no-repeat! important; "> http://vuz.exponenta.ru/PDF/book/GrMaple.pdf /upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini-file_acrobat.gif "target =" _blank "> https://upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini -file_acrobat.gif)! important; background-attachment: initial! important; background-color: initial! important; background-size: initial! important; background-origin: initial! important; background-clip: initial! important; background- position: 100% 50%; background-repeat: no-repeat! important; "> http://eqworld.ipmnet.ru/ru/library/books/Kirsanov2007ru.pdf

задачники

• Мельников О.І. /upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini-file_acrobat.gif "target =" _blank "> https://upload.wikimedia.org/wikipedia/commons/2/23/Icons-mini -file_acrobat.gif)! important; background-attachment: initial! important; background-color: initial! important; background-size: initial! important; background-origin: initial! important; background-clip: initial! important; background- position: 100% 50%; background-repeat: no-repeat! important; "> Цікаві завдання з теорії графів. - НТООО "ТетраСистемс" , 2001. - С. 144.

Примітки

1. ↑ Г. С. Яблонський, В. І. Биков, А. Н. Горбань, Кінетичні моделі каталітичних реакцій , Новосибірськ: Наука (Сиб. Відділення), 1983.- 255 c.
2. ↑ Курейчик В. М., Глушань В. М., Щербаков Л. І. Комбінаторні апаратні моделі і алгоритми в САПР. М .: Радио и связь, 1990. 216 с.

Див. також

Математика Частина 1 - Мілетська школа
Частина 2 - Гумор. Математіка.1
Частина 3 - Математика. Великий енциклопедичний словник.
Частина 4 - Теорія графів
Частина 5 - безліч Мандельброта
Частина 6 - геометрія Лобачевського
...
Частина 9 - Посилання на візуалізації
Частина 10 - MOND. МОНД. Модифікована ньютонівська динаміка
Частина 11 - Аномалія "Піонерів"