1. важливість інтегралів
2. Обчислення інтегралів в вузлі Derived Values
3. Обчислення просторового і тимчасового інтеграла для демо-моделі з області теплопередачі
4. Обчислення просторового інтеграла з використанням операторів вузла Component Coupling
5. Обчислення невизначеного інтеграла за допомогою оператора інтегрування
6. Обчислення просторового інтеграла за допомогою додаткового фізичного інтерфейсу
7. Обчислення тимчасового інтеграла за допомогою вбудованих операторів
8. Обчислення тимчасового інтеграла за допомогою додаткового фізичного інтерфейсу
9. Обчислення інтеграла від аналітичних функцій та виразів

Інтегрування - один з найважливіших математичних інструментів, особливо в чисельному моделюванні. Наприклад, диференціальні рівняння в приватних похідних зазвичай виводяться з інтегральних рівнянь збереження. Коли виникає необхідність чисельного рішення рівняння в приватних похідних, інтегрування також грає важливу роль. У цій статті наведено огляд методів і підходів інтегрування, доступних в COMSOL Multiphysics, а також конкретні приклади їх використання.

важливість інтегралів

У COMSOL використовується метод кінцевих елементів , Який перетворює описує певний процес рівняння в приватних похідних в інтегральне рівняння - іншими словами, в слабку форму (weak form). При детальному і глибокому вивченні формулювань, які використовуються в інтерфейсах COMSOL, ви виявите, що безліч граничних умов реалізовані через інтеграли. В якості найбільш характерних прикладів можна привести умови Total heat flux (Загальний тепловий потік) або Floating potential (Плаваючий потенціал). Обчислення інтегралів також грає ключову роль в процесі обробки поста результатів, оскільки COMSOL розраховує велика кількість допоміжних величин через інтеграли, наприклад енергію електричного поля, швидкість потоку або загальний тепловий потік. Зрозуміло, користувачі вільні використовувати інтегрування в COMSOL в своїх цілях, і в цій статті ми пояснимо вам, як це робити максимально ефективно.

Обчислення інтегралів в вузлі Derived Values

Інтеграл загального вигляду має форму

\ Int_ {t_0} ^ {t_1} \ int _ {\ Omega} F (u) \ \ mathrm {d A} \ mathrm {d} t

де [t_0, t_1] - це часовий інтервал, \ Omega - це просторова область, а F (u) - це довільне вираз, що включає залежну змінну u і довільні функції від неї, в тому числі похідні по простору, часу, а також будь-який іншої величини.

Найбільш зручний спосіб обчислення інтегралів - використання вузла Derived Values ​​(Розрахунок виразів) в розділі Results (Результати) стрічки Ribbon або дерева моделі (Лента Ribbon відсутня в тому випадку, якщо ваш комп'ютер працює не під управлінням ОС Windows®).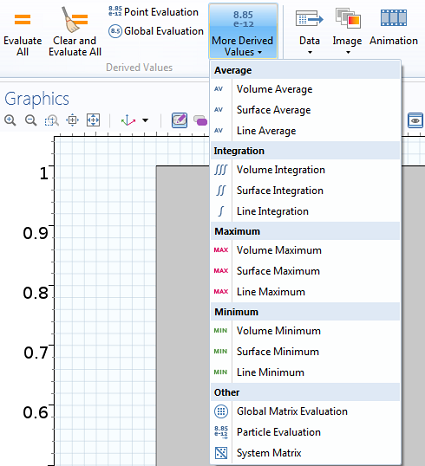

Додавання операцій розрахунку просторових інтегралів за обсягом, поверхні або лінії в вузлі Derived Values (Розрахунок виразів)

Ви можете звернутися до будь-якого доступного рішенням, вибравши відповідний набір даних (data set). В поле Expression (Вираз) вводиться подинтегральная функція, що включає залежні або похідні змінні. Для даних розрахунку в тимчасовій області просторовий інтеграл обчислюється на кожному часовому кроці. В якості альтернативи, у вікні Settings (Настройки) вузла Data Series Operations (Операції з масивами даних) можна вибрати опцію Integral (Інтегрування), що дозволить обчислити загальний просторово-часової інтеграл.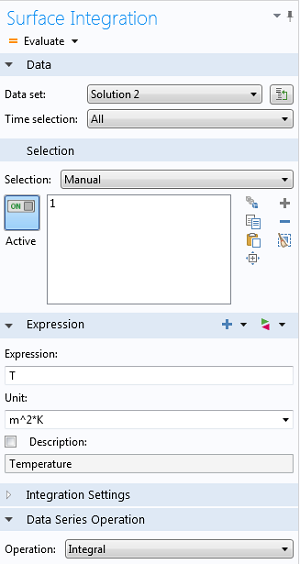

Приклад налаштувань обчислення інтегралів по поверхні (Surface Integration) з додатковим обчисленням інтеграла за часом в розділі Data Series Operations.

Оператор Average (Усереднення) - ще одна операція в розділі Derived Values, пов'язана з обчисленням інтегралів. Оператор обчислює інтеграл і ділить його на обсяг, площа або довжину обраної області. Операція Average у вузлі Data Series Operations аналогічно вводить поділ на тривалість часового діапазону. Оператори вузла Derived Values ​​- важливий інструмент, проте їх можна використовувати тільки під час обробки поста, а значить з їх допомогою можна розрахувати далеко не будь-який інтеграл. Саме тому в COMSOL представлені інші більш потужні та гнучкі інструменти для обчислення інтегралів. Ми продемонструємо їх роботу на представленому нижче модельному прикладі.

Обчислення просторового і тимчасового інтеграла для демо-моделі з області теплопередачі

Розглянемо просту модель теплопередачі: двовимірний одиничний квадрат з алюмінію в (x, y) -плоскості. Температура верхньої і правої сторін постійна і дорівнює кімнатній (293.15 K), в той час як для лівої і нижньої межі заданий загальний входить тепловий потік (General inward heat flux), що становить 5 000 W / m ^ 2. Стаціонарне та нестаціонарне рішення (в момент часу 100 секунд) представлені на ілюстраціях нижче.

Обчислення просторового інтеграла з використанням операторів вузла Component Coupling

Оператори вузла Component Coupling (Сполучення компонентів) використовуються в тих випадках, коли, наприклад, в одному вираженні об'єднуються кілька інтегралів, або інтеграли потрібні в процесі обчислень, або потрібно безліч контурних інтегралів. Оператори даного вузла визначаються в розділі Definitions (Визначення). На цьому етапі режультат використання оператора не прораховується, а вказуються лише їх назва і вибірки областей.

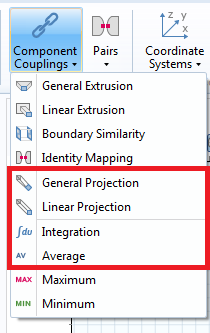
Додавання операторів через вузол Component Couplings

У нашому прикладі ми для початку хочемо обчислити просторовий інтеграл для стаціонарного розподілу температури, що дорівнює

\ Int _ {\ Omega} T (x, y) \ \ mathrm {d} x \ mathrm {d} y = 301.65

У пакеті COMSOL оператор обчислення інтеграла за замовчуванням отримує ім'я intop1.

Тепер давайте розглянемо, як оператор інтегрування може використовуватися безпосередньо в процесі розрахунку моделі. З його допомогою ми могли б, наприклад, з'ясувати, яка нагрівальна потужність буде потрібно для отримання середньої температури 303.15 К, тобто температури, на 10 К нижчою від температури навколишнього середовища. Перш за все нам необхідно обчислити різницю між необхідним і дійсним середніми значеннями. Середнє значення обчислюється шляхом ділення інтеграла від T на інтеграл від постійної функції 1, який дорівнює площі області. Неважко здогадатися, що обчислення подібного виду легко виконати за допомогою представленого в COMSOL оператора Average (Усереднення), см. Коментарі вище. За замовчуванням цей оператор отримує назву aveop1. Зверніть увагу, що середнє значення для області в нашому прикладі збігається з інтегралом, тому що область має одиничну площу. Відповідна різниця дорівнює

303.15- \ int _ {\ Omega} T (x, y) \ mathrm {d} x \ mathrm {d} y = 1.50

Далі нам необхідно знайти значення General heat flux (Загальний тепловий потік) на лівій і нижній межах, при якому була б досягнута необхідна середня температура. Для цього ми введемо додатковий ступінь свободи під назвою q_hot і додаткове обмеження в якості глобального рівняння (Global Equation). Загальний входить тепловий потік (General inward heat flux) тоді перезадать через змінну q_hot.

Додавання додаткової міри свободи (змінної) і глобального рівняння, для неяного підбору середньої температури, що дорівнює 303.15 K.

Рішення даної поєднаної системи за допомогою стаціонарного дослідження дає значення q_ {hot} = 5 881.30 W / m ^ 2. Тобто отримане значення можна задати в якості граничного умови для загального вхідного теплового потоку, щоб середня температура в даній області стала дорівнює 303.15 К.

Обчислення невизначеного інтеграла за допомогою оператора інтегрування

У своїх зверненнях до служби підтримки користувачів часто ставлять одне і те ж питання: як розрахувати невизначений просторовий інтеграл? Для цієї мети нам також знадобиться оператор інтегрування, що задається через Component Couplings. Знаходження невизначеного інтеграла - операція, зворотна диференціюванню. Невизначений інтеграл дозволяє обчислювати площі довільних областей, обмежених графіками функцій. Одна з найважливіших прикладних задач - обчислення ймовірностей в статистичному аналізі. Для того щоб це продемонструвати, ми зафіксуємо y = 0 і позначимо невизначений інтеграл від T (x, 0) як u (x). Це означає, що \ frac {\ partial u} {\ partial x} = T (x, 0). Тоді невизначений інтеграл має вигляд

u (\ bar x) = \ int_0 ^ {\ bar x} T (x, 0) \ mathrm {d} x

Тут ми використовуємо \ bar x, щоб відрізняти змінну інтегрування від зовнішньої змінної. На відміну від наведених вище інтегралів, результатом інтегрування є функція, а не скалярна величина. Нам необхідно вказати для ПО, що для кожного значення \ bar x \ in [0,1] відповідне значення u (\ bar x) обчислюється за допомогою інтеграла. У середовищі COMSOL це можна легко зробити всього за три кроки. По-перше, потрібно логічне вираз для переписування інтеграла у вигляді

u (\ bar x) = \ int_0 ^ 1T (x, 0) \ cdot (x \ leq \ bar x) \ \ mathrm {d} x

По-друге, нам знадобиться оператор обчислення інтеграла, який буде діяти на нижній межі області з прикладу. Давайте позначимо його як intop2. По-третє, ми повинні відрізняти змінну інтегрування від зовнішньої змінної. Прийняті позначення для такого випадку: x називається джерелом (source), а \ bar x - точкою призначення (destination). При використанні операторів інтегрування доступний вбудований оператор dest, який дозволяє явно оголошувати, що відповідне вираз не відноситься до змінних інтегрування. Точніше, це означає, що в COMSOL \ bar x = dest (x). Об'єднавши логічне вираз з оператором dest, ми отримаємо вираз виду T * (x <= dest (x)), яке є саме тим вхідним виразом, яке потрібно для intop2. Об'єднавши всі разом, ми можемо обчислити невизначений інтеграл, скориставшись виразом intop2 (T * (x <= dest (x))). Результат цієї операції можна проілюструвати наступним графіком:

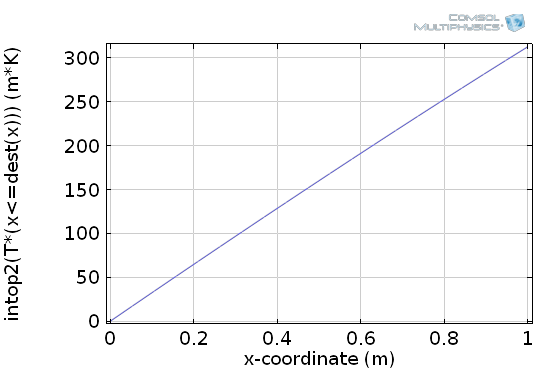
Як побудувати графік невизначеного інтеграла за допомогою оператора інтегрування, оператора dest і логічного виразу.

У пакеті COMSOL додатково доступні ще два оператора обчислення інтеграла, а саме загальна проекція (general projection) і лінійна проекція (linear projection). Ці оператори можна використовувати для отримання безлічі контурних інтегралів в будь-якому напрямку в області. Іншими словами, обчислення інтеграла проводиться тільки уздовж одного виміру. В результаті ми отримуємо функцію розмірності на одиницю менше, ніж розмірність області. Для двовимірного прикладу результатом буде одномірна функція, яка може бути розрахована на будь-якому кордоні. Більш детальна інформація про використання даних операторів буде представлена ​​в одній з наступних публікацій в нашому компоративного блозі.

Обчислення просторового інтеграла за допомогою додаткового фізичного інтерфейсу

Найбільш гнучким способом обчислення просторових інтегралів є техніка з додаванням додаткового PDE-інтерфейсу. Давайте згадаємо приклад вище з невизначеним інтегралом і припустимо, що ми хочемо обчислити невизначений інтеграл не тільки для y = 0. Дане завдання може бути сформульована у вигляді диференціального рівняння в приватних похідних

\ Frac {\ partial u} {\ partial x} = T (x, y)

з граничною умовою типу Діріхле u = 0 на лівій межі. Розрахунок такого рівняння найпростіше реалізувати в фізичному (математичному) інтерфейсі Coefficient Form PDE (Диференціальне рівняння в приватних похідних, коефіцієнтний форма запису), який зажадає наступних установок:

Обчислення просторового інтеграла за допомогою додаткового PDE-інтерфейсу.

Залежна змінна u являє собою невизначений інтеграл по x і доступна в процесі розрахунку моделі і в постобробці. Крім гнучкості, додатковою перевагою даного підходу є точність, так як інтеграл розраховувати не допоміжними інструментами на основі вже певного розподілу змінної, а безпосередньо в процесі розрахунку з урахуванням алгоритмів оцінки похибок і т.п.

Обчислення тимчасового інтеграла за допомогою вбудованих операторів

Ми вже згадували вузол Data Series Operations, який можна використовувати для обчислення інтеграла за часом. Інший вкрай корисний спосіб обчислення інтеграла за часом забезпечується вбудованими операторами timeint і timeavg для обчислення інтеграла або середнього значення за часом, відповідно. Дані інструменти доступні при постобробці результатів, використовуються для обчислення інтеграла від будь-якого виразу (залежить від часу) на заданому часовому інтервалі. У нашому прикладі ми розрахуємо середнє значення температури в діапазоні від 90 до 100 секунд, тобто:

\ Frac {1} {10} \ int_ {90} ^ {100} T (x, y, t) \ \ mathrm {d} t

На поверхневому графіку нижче представлений результуючий інтеграл, що є функцією просторових змінних (x, y):

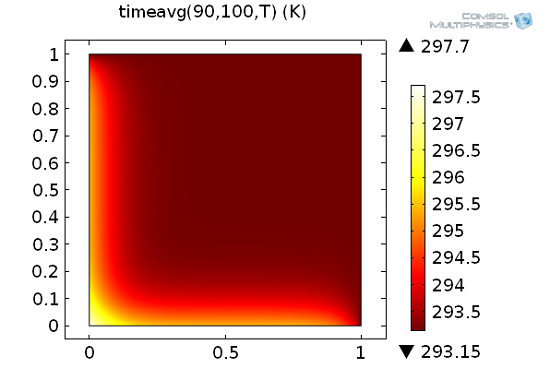
Використання оператора timeavg - оператора обчислення інтеграла за часом.

Схожі оператори існують для обчислення інтегралів на сферичних зонах, а саме ballint, circint, diskint і sphint.

Обчислення тимчасового інтеграла за допомогою додаткового фізичного інтерфейсу

У разі якщо тимчасові інтеграли потрібно використовувати безпосередньо в моделі в процесі розрахунку, вам буде необхідно задати їх як додаткові залежні змінні. Аналогічно представленому вище прикладу з інтерфейсом Coefficient Form PDE, це можна зробити, додавши ODE-інтерфейс з розділу Mathematics. Припустимо, наприклад, що на кожному часовому кроці потрібно обчислювати інтеграл від величини загального теплового потоку на проміжку від старту до поточного моменту, який показує накопичену енергію. Змінна для загального теплового потоку розраховується в COMSOL автоматично і називається ht.tfluxMag. Інтеграл може бути обчислений як додаткова залежна змінна за допомогою вузла Distributed ODE (Розподілене звичайне диференціальне рівняння) інтерфейсу Domain ODEs and DAEs. Правою частиною (від джерела членом) для доменного ОДЕ повинна виступати подинтегральная функція, що і показано на ілюстрації нижче.

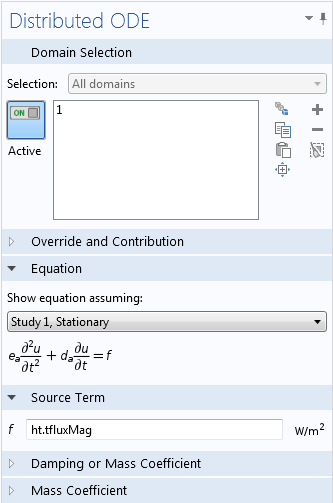
Використання додаткового ODE-інтерфейсу для обчислення інтеграла за часом.

У чому користь подібної техніки? Отриманий інтеграл можна повторно використовувати в інших фізичних інтерфейсах, поля в яких можуть залежати від накопиченої в системі енергії. Більш того, отриманий резултат буде мгноменно доступний для всіх видів обробки поста, що зручніше і швидше, ніж використання вбудованих операторів. Рекомендуємо ознайомиться з моделлю Carbon Deposition in Hetereogeneous Catalysis (Освіта сажових відкладень при гетерогенному каталізі) , В якій ОДЕ в області використовується для обчислення пористості каталізатора при наявності хімічних реакцій у вигляді нестаціонарної польовий змінної.

Обчислення інтеграла від аналітичних функцій та виразів

До сих пір ми демонстрували, яким чином обчислювати інтеграл від шуканих змінних в процесі розрахунку або при постобробці. Але не торкалися випадку взяття інтегралів від аналітичних функцій або виразів. Для цієї операції в середовищі COMSOL доступний вбудований оператор integrate (expression, integration variable, lower bound, upper bound).

Вираз може бути будь-якою одновимірну функцію, наприклад sin (x). При цьому допускається включення додаткових змінних, наприклад sin (x * y). Другий параметр визначає, з якої змінної обчислюється інтеграл. Наприклад, integrate (sin (x * y), y, 0,1) видає функцію змінної x, тому що інтегрування виконується тільки за змінною y. Зверніть увагу, що даний оператор також може використовуватися для роботи з аналітичними функціями, заданими в вузлі Definitions (Визначення) поточного компонента.

Матеріали для подальшого вивчення